Используются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение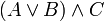 
означает, что сначала выполняется логическое сложение 
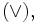а затем — логическое умножение 
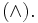Наряду с квадратными скобками используются также для записи компонент векторов:
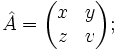
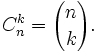
Круглые скобки в математике используются также для выделения аргументов функции: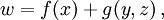 
для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:
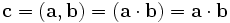
(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение:
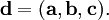
При обозначении диапазона чисел круглые скобки обозначают, что числа, которые находятся по краям множества не включаются в это множество. То есть запись А = (1;3) означает, что в множество включены числа, которые 1(открытый) интервал.
В химических формулах круглые скобки применяются для выделения повторяющихся функциональных групп, например, (NH4)2CO4, Fe2(SO4)3, (C2H5)2O. Также скобки используются в названиях неорганических соединений для обозначения степени окисления элемента, например, хлорид железа(II), гексацианоферрат(III) калия.
Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках.
Во многих языках программирования используются круглые скобки для выделения конструкций. Например, в языках Паскаль и Си в скобках указываются параметры вызова процедур и функций, а в Лиспе — для описания списка.
Квадратные скобки
В лингвистике употребительны для обозначения транскрипции в фонетике или границ составляющих в синтаксисе.
Квадратными скобками в цитатах задают авторский текст, который проясняет контекст цитаты. Например, «Их [заложников] было около 100 человек».
Квадратными скобками в математике могут обозначаться:
- Операция взятия целой части числа.
- Для задания приоритета операций (аналогично круглым) в качестве скобок «второго уровня» — так легче различать вложенность скобок, например: [(2+3)·4]².
- Векторное произведение векторов: c=[a,b]=[a×b]=a × b.
- Закрытые сегменты; запись [1;3] означает, что в множество включены числа
. В этом случае не соблюдается правило парности скобок, например, закрытый слева и открытый справа сегмент может быть обозначен как [x,y[ или [x,y). - Коммутатор
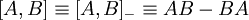и антикоммутатор 
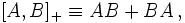хотя для последнего иногда используют фигурные скобки без нижнего индекса. - Одинарная квадратная скобка объединяет совокупность уравнений или неравенств (чтобы совокупность выполнялась, достаточно, чтобы выполнялось любое из уравнений).
В химии квадратными скобками обозначают комплексные анионы и катионы, например: Na2[Fe(NO)(CN)5], [Ag(NH3)2] + . Также, по номенклатуре IUPAC в квадратные скобки заключается количество атомов в мостиках между двумя атомами в названии органических полициклических соединений, например: бицикло[2,2,2]октан.
В вики-разметке двойные квадратные скобки используются для внутренних ссылок, перенаправлений, категорий и интервики, одинарные — для внешних.
В программировании чаще всего применяются для указания индекса элемента массива.
Часто квадратные скобки используются для обозначения необязательности, например, параметров командной строки (см. подробнее в статье Форма Бэкуса — Наура).
Фигурные скобки
Фигурными скобками в одних математических текстах обозначается операция взятия дробной части, в других — они применяются для обозначения приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок). Фигурные скобки применяют для обозначения множеств. Одинарная фигурная скобка объединяет системы уравнений или неравенств. В математике и классической механике фигурными скобками обозначается оператор специального вида, называемый скобками Пуассона: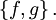 
Как уже было сказано выше, иногда фигурными скобками обозначают антикоммутатор.
В вики-разметке двойные фигурные скобки применяются для шаблонов.
В программировании фигурные скобки являются или операторными (Си, C++, Perl и комментарием (Паскаль), могут также служить для образования списка (в Сетл).
Угловые скобки
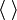
В математике угловыми скобками обозначают кортеж, реже — скалярное произведение в предгильбертовом пространстве, например:
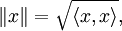
В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как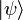 
(кет-вектор) и 
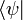(бра-вектор), их скалярное произведение как 
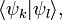матричный элемент оператора А в определённом базисе как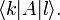 
Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например,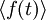 
— среднее значение по времени от величины f.
В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте —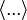 
.
Типографика
В HTML / программировании) для записи угловых скобок используют схожие по написанию парные знаки арифметических отношений неравенства « » .
В типографике же угловые скобки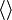 
являются самостоятельными символами. От « » их можно отличить по бо́льшему углу между сторонами — 
.
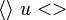В ТеХе для записи угловых скобок используются команды «langle» и «
angle».
В стандартной пунктуации китайского, японского и корейского языков используются специальные символы — шевроны (англ. chevron ), схожие по написанию с угловыми скобками — для горизонтальной 〈 и 〉 или 《 и 》 и традиционной вертикальной печати — ︿ и ﹀ или ︽ и ︾ .
ASCII-тексты
В некоторых языках разметки, напр., HTML, XML угловыми скобками выделяют теги.
В вики-разметке также можно использовать HTML-разметку, например комментарии — « », которые видны только при редактировании статьи.
В программировании угловые скобки используются редко, чтобы не создавать путаницы между ними и знаками отношений (« »). Например в Си угловые скобки используются в директиве препроцессора #include вместо кавычек, чтобы показать что включаемый заголовочный файл необходимо искать в одном из стандартных каталогов для заголовочных файлов, например в следующем примере:
файл stdio.h находится в стандартном каталоге, а myheader.h — в текущем каталоге (каталоге исходника программы).
В некоторых текстах, сдвоенные парные « » используются для записи кавычек-ёлочек, например — >.
Косые скобки
Появились на пишущих машинках для экономии клавиш.
В программировании на языке Си косые скобки вместе с дополнительным знаком «*» обозначают начало и конец комментария:
Прямые скобки
Используются в математике для обозначения модуля числа или вектора, определителя матрицы:
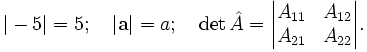
Двойные прямые скобки
Используются в математике для обозначения нормы элемента линейного пространства: ||x||; иногда — для матриц:
Откуда взялись скобки в математике? Скобки, или, как их еще называют, особые "знаки препинания", в математическом языке позволяют менять последовательность арифметических действий. Они вошли в употребление в 16 – начале 17 веков.
Первыми появились квадратные скобки в математике "[ ]", их ввел в 1550 г. Рафаэль Бомбелли (1530–1572), итальянский математик и инженер-гидравлик, который работал в Болонье.
Появлению круглых скобок "( )" мы обязаны известному итальянскому математику Никколо Тарталье (1500–1557), который родился в бедной семье. Истинная фамилия его неизвестна, и может быть, он и сам не знал ее. Отец его умер рано, оставив жену с тремя детьми. Когда мальчику было шесть лет, его родной город Брешию захватили французские войска. Люди спрятались в соборе, но стены храма не спасли их от кровавой бойни. Никколо повезло – он остался жив, но получил ранение: ему повредили горло, рассекли язык, и мальчик с трудом произносил слова. Поэтому его прозвали "тарталья" – "заика". В школе Никколо проучился лишь 15 дней: мать не смогла платить за учебу. Но мальчик обладал большой настойчивостью и терпением и научился читать сам. Как правило, денег на бумагу не хватало, и Тарталья каждый день ходил на кладбище и писал упражнения и задачи углем на мраморных надгробиях.
Никколо так пристрастился к математике, что самостоятельно достиг небывалых высот; в дальнейшем он сам начал преподавать любимый предмет и стал выдающимся математиком своего времени. Преподавал он в Вероне, Брешии и Венеции. Тарталья вошел в историю науки под именем "человека, сделавшего самого себя". Тарталья написал несколько книг, самая важная из которых была издана в Венеции в 1556 г. под названием "Общие исследования чисел и мер". В ней он впервые применил круглые скобки в математике. Впоследствии, в математике круглые скобки начал использовать математик М. Штифель. Первым стал применять их Ф. Виет, правда, у него они имели вид не скобок, а черты над многочленом. А вот фигурные скобки в математике "< >" появились именно благодаря Виету (в 1593 г.).
Фигурные скобки чаще всего употребляются в математических формулах, где они обычно объединяют группу формул или охватывают выражение, в котором уже были использованы круглые или квадратные скобки. Однако широко фигурные скобки в математике стали применяться позднее в работах Лейбница и Эйлера.
Скобки нашли применение не только в математике. Круглые скобки широко применяются в химии, языках программирования. Всем знакомо использование квадратных скобок для транскрипции в фонетике. Фигурные скобки нашли применение в таких популярных языках программирования, как Си, Jаvа, Паскаль (в комментариях).
Ответ или решение 1
Круглые скобки ставятся тогда, когда крайние числа промежутка не входят в решение. Например, (0; 5) промежуток от нуля до пяти, но числа 0 и 5 не входят в промежуток. Но числа, чуть большие 0 (например, 0,00001) и числа чуть меньшие 5 (например, 4,9999) входят в промежуток. Круглые скобки используются при решении строгих неравенств (когда знак ).
Квадратные скобки ставят, когда крайние числа входят в решение. Промежуток [-1; 8] это числа от -1 до 8 включительно. Квадратные скобки используются при решении нестрогих неравенств (≥ или ≤).
В одном промежутке могут быть и круглая и квадратная скобка. Например, х > -3, но х ≤ 5. Тогда промежуток будет (-3; 5].
